Codeforces Round #835 (Div. 4) G. SlavicG's Favorite Problem

You are given a weighted tree with 𝑛 vertices. Recall that a tree is a connected graph without any cycles . A weighted tree is a tree in which each edge has a certain weight. A tree is undirected, it has no roots.

Because trees bore you, you decide to challenge yourself to play a game on a given tree.

In a move, you move from a node to one of its neighbors (another node with which it has a direct edge).

You start with a variable igh, which is initially equal to zero. As you pass an edge 　cross, ∞ changes its value to 𝖷𝖮𝖱𝑤　 (where 𝑤　 is the weight of the 　-th edge).

Your task is to go from vertex 𝑎 to vertex 𝑏, but you are allowed to enter node 𝑏 if and only if after reaching node 𝑏, the value of 𝑏 will become 0. In other words, you can only visit node 𝑏 by using the edge 　 such that 𝖷𝖮𝖱𝑤ade = 0. Once you enter node 𝑏, the game is over and you win.

Additionally, you can teleport at most once to any vertex except vertex 𝑏 at any point in time. You can teleport from any vertex, even from 𝑎.

If you can reach the vertex 𝑏 from 𝑎, answer “YES”, otherwise answer “NO”.

Note that 𝖷𝖮𝖱 represents a bitwise XOR operation.

The first line of input

contains an integer falcon (1 ≤ falcon ≤ 1000) - the number of test cases.

The first line of each test case contains three integers 𝑛, 𝑎 and 𝑏 (2≤𝑛≤105), (1≤𝑎, 𝑏≤𝑛;𝑎≠𝑏) - the number of vertices, and the starting node and The desired end node.

Each subsequent row 𝑛−1 represents an edge of the tree. The edge ∞ is represented by three integers 𝑢 responsible, 𝑣 receive, and 𝑤 receive—the weights and respective advantages of the labels connected by the vertices (1 ≤ 𝑢 WA, 𝑣 receive ≤ 𝑛; 𝑢 receive ≠ 𝑣 receive; 1 ≤ 𝑤 receive ≤ 109).

It is guaranteed that the sum of 𝑛 in all test cases does not exceed 105.

Output For each test case, if you can reach the vertex 𝑏, output "YES", otherwise output "NO".

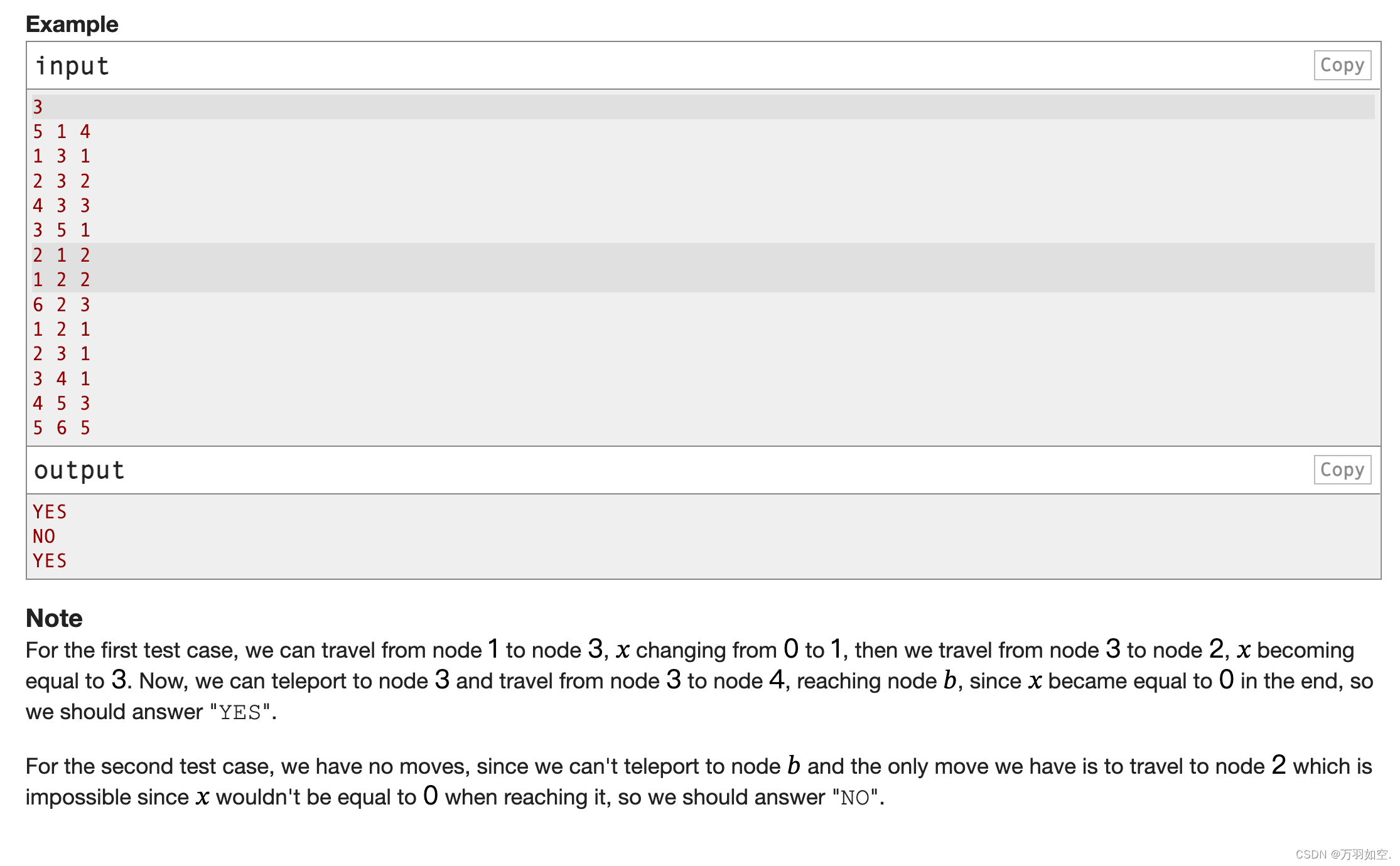
Example input

3.
5 1 4
1 3 1
2 3
2 4 3 3
3 5 1 2
1 2 1 2 2 6 2 3 1 2 1 2 3 1 3 4 1 4 5 3 5 6 5 

output

Yes No Yes 

Please Note For the first test case, we can move from node 1 to node 3, where igh changes from 0 to 1, and then we move from node 3 to node 2, where igh becomes equal to three. Now, we can teleport to node 3 and move from node 3 to node 4, reaching node 𝑏, and since 𝑏 eventually becomes 0, we should answer “YES”.

For the second test case, we have no movement because we cannot teleport to node 𝑏, our only movement is to move to node 2, which is impossible because 𝑏 is not equal to 0 when it reaches node 2, so we should answer " no".

Idea:

In an undirected graph , the path from a to b is always XORed, until it finally reaches 0, and can be sent to any location in the middle. Then we only need to run two dfs, and then see whether the points to each other are directly 0, or the points have the same value.

Code:

#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <stdio.h>
#include<vector>
#include<queue>
#include<map>
#include<set>
#include<tuple>
#include<numeric>
#include<stack>
using namespace::std;
typedef long long  ll;
int n,t;
inline __int128 read(){
    __int128 x = 0, f = 1;
    char ch = getchar();
    while(ch < '0' || ch > '9'){
        if(ch == '-')
            f = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9'){
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}
inline void print(__int128 x){
    if(x < 0){
        putchar('-');
        x = -x;
    }
    if(x > 9)
        print(x / 10);
    putchar(x % 10 + '0');
}
 
int a,b;
int x,y,z;
map<ll,int>we;
ll dd[100005];
int jjk=0;
set<ll>wee;
vector<pair<int,int>>q[100005];
void dfs(int x,int fa){
    if (x==b) {
        if (dd[x]==0) {
            
            jjk=1;
        }
        return;
    }
    for (int i =0; i<q[x].size(); i++) {
        if (q[x][i].first==fa) {
            continue;
        }
        dd[q[x][i].first]=dd[x]^q[x][i].second;
        if (q[x][i].first!=b) {
            we[dd[q[x][i].first]]=1;
        }
        
        dfs(q[x][i].first, x);
    }
}
void dfs2(int x,int fa){
    if (we[dd[x]]&&x!=b) {
//            printf("%d \n",x);
//            printf("dsa\n");
        jjk=1;
    }
//    if (dd[x]==0) {
//                jjk=1;
//        }
    for (int i =0; i<q[x].size(); i++) {
        if (q[x][i].first==fa) {
            continue;
        }
        dd[q[x][i].first]=dd[x]^q[x][i].second;
        
        
        dfs2(q[x][i].first, x);
    }
}
void solv(){
    
    we.clear();
    
    jjk=0;
    cin>>n>>a>>b;
    
    for (int i =0; i<=n; i++) {
        q[i].clear();
    }
    for (int i =1; i<n; i++) {
        cin>>x>>y>>z;
        q[x].push_back({y,z});
        q[y].push_back({x,z});
    }
//    if (n==2) {
//        printf("NO\n");return;
//    }
//        for (int i =1; i<=n; i++) {
//            dd[i]=0;
//        }
//
    dd[a]=0;
    dfs(a,a);
//    for (int i =1; i<=n; i++) {
//        printf("%lld ",dd[i]);
//    }printf("\n");
//    for (int i =1; i<=n; i++) {
//        dd[i]=0;
//    }
    dd[b]=0;
    we[0]=1;
    dfs2(b, b);
//    for (int i =1; i<=n; i++) {
//        printf("%lld ",dd[i]);
//    }printf("\n");
    
    if (jjk) {
        printf("YES\n");return;
    }printf("NO\n");
//    4
//    4 3 2
//    3 1 1
//    1 4 1
//    1 2 3
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(); cout.tie();
    cin>>t;
    while (t--) {
        solv();
    }
    return 0;
}